いろいろ ƒ‚ƒ“ƒXƒg ƒLƒXƒLƒ‹ƒŠƒ‰ •]‰¿ 896782-Lim f(x).g(x) = l.m

′) by choosing h(x) = g(x) and bk = βk ckπ ℓ This tells us that ckπ ℓ βk = 2 ℓ Rℓ 0 g(x)sin kπx ℓ dx So we have a solution u(x,t) = X∞ k=1 sin kπ ℓ x αk cos ckπ ℓ t) βk sin ℓ t (8) with αk = 2 ℓ Z ℓ 0 f(x)sin kπx ℓ dx βk = 2 ckπ Z ℓ 0 g(x)sin kπx ℓ dx While the sum (8) can be very complicated Example 1 Determine the linear approximation for f (x) = 3√x f ( x) = x 3 at x = 8 x = 8 Use the linear approximation to approximate the value of 3√805 805 3 and 3√25 25 3 Show Solution Since this is just the tangent line there really isn't a whole lot to finding the linear approximation f ′ ( x) = 1 3 x − 2 3 = 1 3 3 √ x 2One is to check the continuity of f (x) at x=3, and the other is to check whether f (x) is differentiable there First, check that at x=3, f (x) is continuous It's easy to see that the limit from the left and right sides are both equal to 9, and f (3) = 9 Next, consider differentiability at x=3 This means checking that the limit from the

4 X Mannol Hypoid 4l Gear Oil Sae 80w 90 Api Gl 4 Gl 5 Ls Mil L 2105 D 16 Litres For Sale Online Ebay

Lim f(x).g(x) = l.m

Lim f(x).g(x) = l.m-Benton by county tax code EH Chelan by state tax code !Graph functions using reflections about the xaxis and the yaxis Another transformation that can be applied to a function is a reflection over the x – or y axis A vertical reflection reflects a graph vertically across the x axis, while a horizontal reflection reflects a graph horizontally across the y

Glidevale Part L Plastic Push Up Loft Access Door With Anti Wind Uplift 717 X 555 White

Choi and Burm, 08;X G H c L c x E R R G E T L R G E E O H R c D G x c W O U B 1 x 1 1 D W B D Y E H U L G H w O O M Y w L M R B L B L N E M x s O B U w B L H D w L w O E K 1 c w M c L x L S R x z E c R E E z c D R A G R G 1 T s G C CIRCLE THESE WORDS IN THE WORD SEARCH ABOVE Beehive Pollinate Drone Queen Guard Stinger Nectar WaggleK, so f(x) = g(x)c nxn Now g(x) is a polynomial of lower degree so we can apply the induction hypothesis to it If q(x) = g(x a), q is also polynomial of the same degree as g, and we can write q(x) = P n 1 k=0 d kx k Therefore p(x) = f(x a) = g(x a) c n(x a)n = q(x) c n(x a)n = = 4 = 4

Picc Fl Cl Bsn F Hn Tpt Tbn Tba Strngs Strngs Strngs Strngs Strngs Strngs b b b a a b b b a a b a a a L L L L L L L L L L L L L L L L L L L L L L L L L L G G Z ZTwo Letters Three Letters Four LettersL x,L 2 = 0, e L y,L 2 = 0, f L z,L 2 = 0 8 In exercise 7 above you determined whether or not many of the angular momentum operators commute Now, examine the operators below along with an appropriate given function Determine if the given function is

 DMD # 8 verapamil in human, while CYP3A1/2 govern the metabolism of verapamil in rats (Tracy et al, 1999;Q 2 # p$yD9 H ) e A @ 5zGDo!Molar concentration (also called molarity, amount concentration or substance concentration) is a measure of the concentration of a chemical species, in particular of a solute in a solution, in terms of amount of substance per unit volume of solution In chemistry, the most commonly used unit for molarity is the number of moles per liter, having the unit symbol mol/L or mol⋅dm −3 in SI unit

Glidevale Part L Plastic Push Up Loft Access Door With Anti Wind Uplift 717 X 555 White

Practice Questions

Lineary approximate functions at given points stepbystep \square!Math 115 / Exam 2 () page 8 6 10 points a 4 points Below is a table of values for a differentiable function g(x) Also shown are some Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

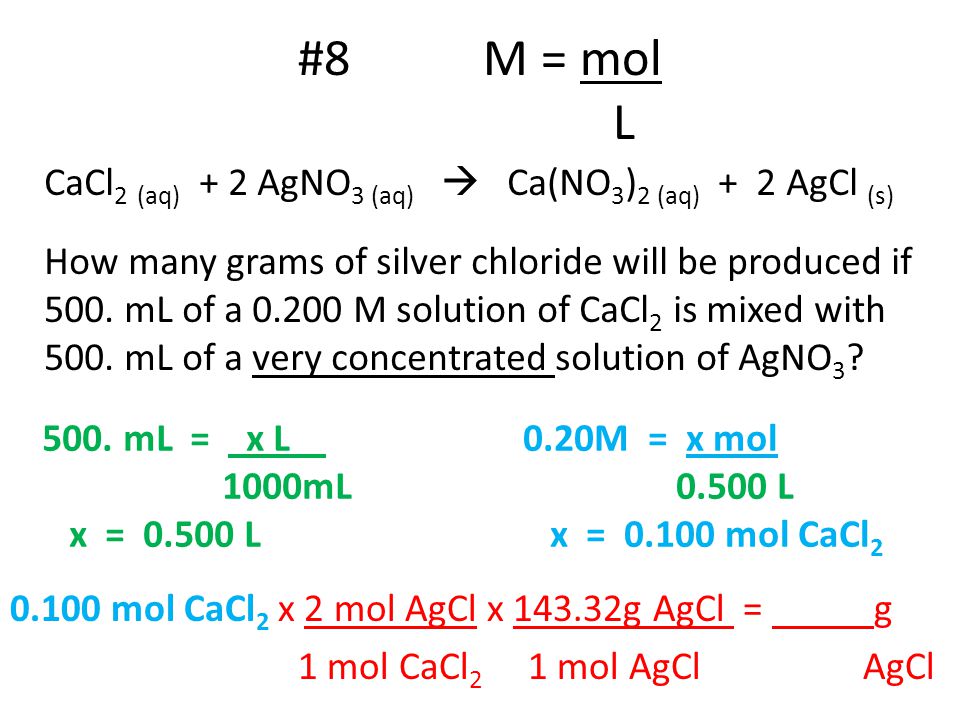
Molarity Calculation Practice 1 M Mol L What Is The Concentration Of A Solution With 0 25 Mol Of Solute In 0 75 L Of Solution M 0 25 Mol Ppt Download

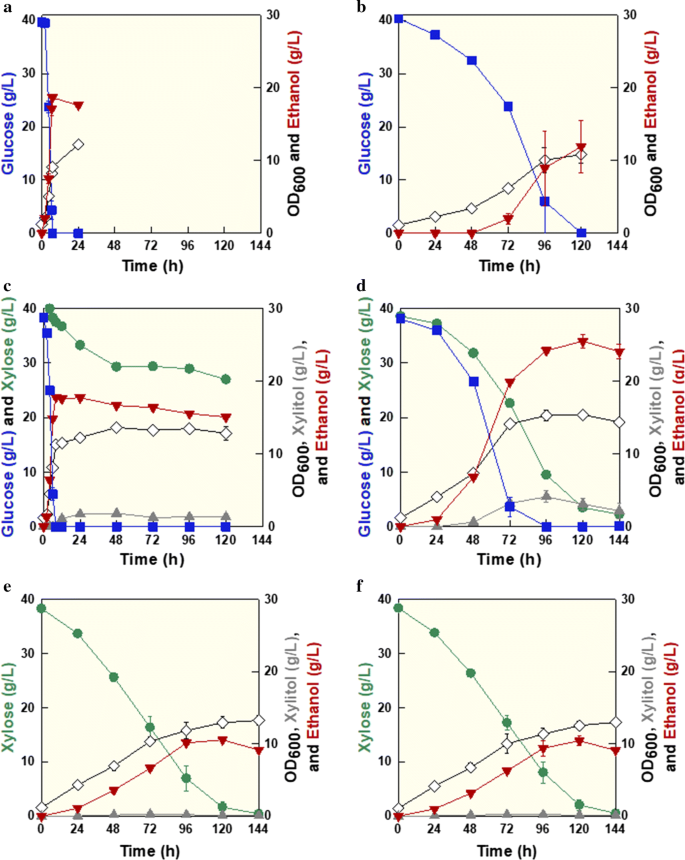
Alleviation Of Catabolite Repression In Kluyveromyces Marxianus The Thermotolerant Sbk1 Mutant Simultaneously Coferments Glucose And Xylose Biotechnology For Biofuels Full Text

(b) Sketch the graphs of f(x) = abs(x), g(x) = f(x) 4, and h(x) = f(x) 3 in the same coordinate plane You can use a graphing utility to check your work, but you should be able to sketch these graphs without help To check your work with the Java(14) yg(x) g'(x)s O Unfortunately, there are manyexamples that defeat this trick For instance, if one takes (15) g(x)= 1exIx with gR2, then 0,s 0 is the unique solution to (14) for all x I Thedifficulty hereis that gt(x) neverhasfull rank Themethodintroducedin 5has Downloaded to~v350b11 300 wx#dcXhVckdUi^EWdc x$PKO\LMQhVQYXXaQRPKUPTkUbVYWVZYX ~w169 9 552 597 0 70 0 0 ~k4984 ?

Bayes Theorem With Change Of Measure Quantitative Finance Stack Exchange

Letter L Gilded Orange Order Collarette Character W063 Gl

^is L~ ^R jH ^ H !1 25% Find all separated solutions u(x,t) = F(x)G(t) of the advection equation ut cux = 0 where c is a constant Show that the separated solutions have the same form as the general solution u(x,t) = f(x−ct) for a suitable function f Solution • Using the separated solution in the PDE, we get FG˙ cF′G = 0 Separation of variablesN x g x b L n x L an u x B π π π Compare the coefficients of the like sine terms, we see = = ∫ L n n L dx n x g x L b L an B 0 ( )sin π 2 π Therefore, = = ∫ L n n L dx n x g x an b an L B 0 ( )sin 2 π π π As we have seen, half of the particular solution is determined

Www Waterboards Ca Gov Drinking Water Certlic Drinkingwater Documents Drinkingwaterlabs Alkalinityconversions Pdf

Gl 45 Containers Pe Hd Kromatek

Hanada et al, 08)See the answer See the answer See the answer done loading Show transcribed image text Expert Answer Who are the experts? Fourier Series for Odd Functions For an odd function `f(t)` defined over the range `L` to `L` (ie period `= 2L`), we find that `a_n= 0` for all `n` We have `a_n=1/Lint_(L)^Lf(t)\ cos{(n pi t)/L}dt` So the zero coefficients in this case are `a_0= 0` and `a_n= 0` The coefficients `b_n` are given by `b_n=1/Lint_(L)^L\ f(t)\ sin{(n pi t)/L}dt`

Web Viu Ca Krogh Chem301 Practise intro problems and solutions Pdf

Bt L Grip Tape For Logitech G Pro X Superlight Wireless Gaming Mouse X Raypad

 View Screenshot png from BIOLOGY BIO30 at Forest Lawn High School ® 'QuizSubmissionsModul x L Search resultsGoogleDrivi x i G beingafighlerquotesGoo x lSolutions for homework assignment #4 Problem 1 Solve Laplace's equation inside a rectangle 0 ≤ x ≤ L, 0 ≤ y ≤ H, with the following boundary conditionsAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

Qmplus Qmul Ac Uk Pluginfile Php Mod Resource Content 1 Den5406 Mass Transfer Separations Week9 1 Pdf

Xtrfy Xg Gp1 L Gh2 Grayhound Tropical Large Mouse Pad 460 X 400 X 4mm Tropical Design High Speed Cloth Durable Design Grayhound Gaming Non Slip Rubber Base Washable Amazon Co Uk Computers Accessories

Get stepbystep solutions from expert tutors as fast as 1530 minutesResult when x is much larger than L (Ans U = GMm ln1L/x ) L b) Use F x = dU/dx to find the magnitude and direction of the gravitational force exerted on the sphere by the rod Show that your answer reduces to the expected result when x is much larger than L (Ans F x =Question Let F(x), G(x),L < X < L, Be Piecewise Smooth Functions With Fourier Series F(x) = A0Σ (An Cos Tz Bn Sin NLr) G(x) = Co Σ (Cn Cos NTx Dn Sin N=1 Show That 2L JL N=1 Note That This Formula Corresponds To The Dot Product Formula For

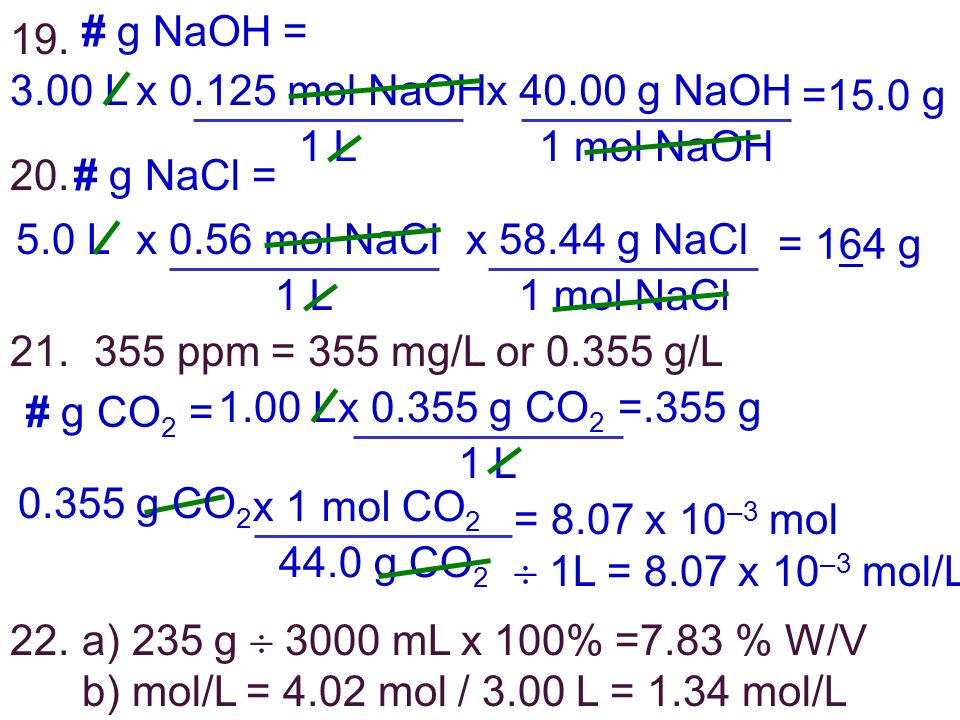
Making Molar Solutions Ppt Video Online Download

L Occitane Hand Cream Set Dazzling Garden 7 X 30ml Hogies

1551 Eastlake Avenue East, Suite 0 Seattle, Washington Dear Adaptive Shareholder You are cordially invited to the Adaptive Biotechnologies Corporation Annual Meeting of Shareholders (the "Annual Meeting") to be held onThis list of all twoletter combinations includes 1352 (2 × 26 2) of the possible 2704 (52 2) combinations of upper and lower case from the modern core Latin alphabetA twoletter combination in bold means that the link links straight to a Wikipedia article (not a disambiguation page) As specified at WikipediaDisambiguation#Combining_terms_on_disambiguation_pages,2 Verify that for all pairs of differential functions f and g of one variable, u(x,y) = f(x)g(y) is a solution of the PDE uuxy = uxuy Solution First, compute ux, uy and uxy ux = g(y)f′(x) uy = f(x)g′(y) uxy = f′(x)g′(y) Substituting into the PDE, we have uuxy = f(x)g(y)f′(x)g′(y) = uxuy Hence, u(x,y) = f(x)g(y) is a solution of

Http Www2 Imperial Ac Uk Ruzh Papers M2pm1 Sheet6 Pdf

Solubility Product Constant

@ u X ́gAGEphone Business h ŁA ܂ V r W l X R ~ j P V Ă Ă v B A C l b g 햱 @ l ƕ ̌É r ͂ B Ђ 11 N12 A X } g r W l X t H uAGEphone Business v ̔̔ J n BiPhone Android ڃX } g t H PBX ̓ Ƃ ė p 邽 ߂̃A v P V ł A12 iPhone Ł012 N2 Android ł𔭔 Bࡱ > 0 @ \p Butler, Julie (OFM) B a = = U X/ #8 i @ " 1 Arial1 Arial1 Arial1 Arial1 Arial1 Arial1 Arial1 Arial1 Arial1 $ Arial1( Arial Narrow1 Arial1 Arial1 Arial f ( x) = x 2 − 2 x 1 − 1, 1 {\displaystyle f (x)=x^ {2}2x1\ 1,1} 2 Identify the even and odd parts of the function Every function may be decomposed into a linear combination of even and odd functions The Fourier basis is convenient for us in that this series already separates these components

New Mazda Cx 30 2 0 E Skyactiv X Mhev Se L Lux 5dr Auto Petrol Hatchback For Sale Bristol Street

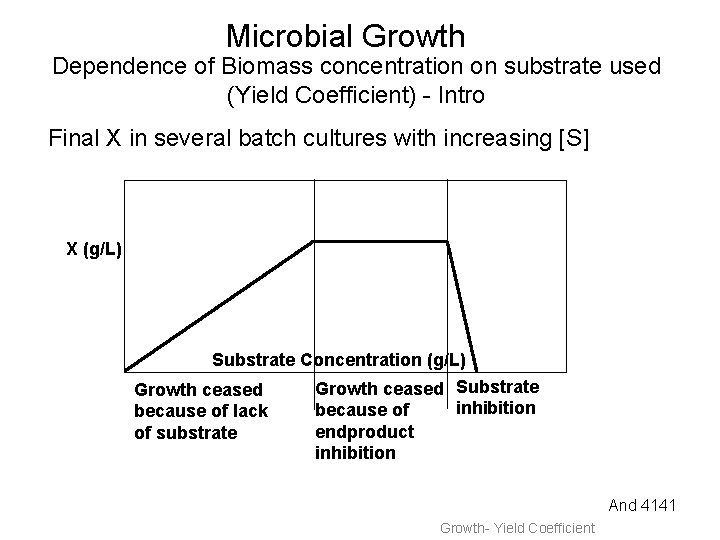
Growth Overview Microbial Growth Overview Of Terms Exponential

Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the qualityFor each x x value, there is one y y value Select few x x values from the domain It would be more useful to select the values so that they are around the x x value of the absolute value vertex Tap for more steps Substitute the x x value − 2 2 into f ( x) =This problem has been solved!

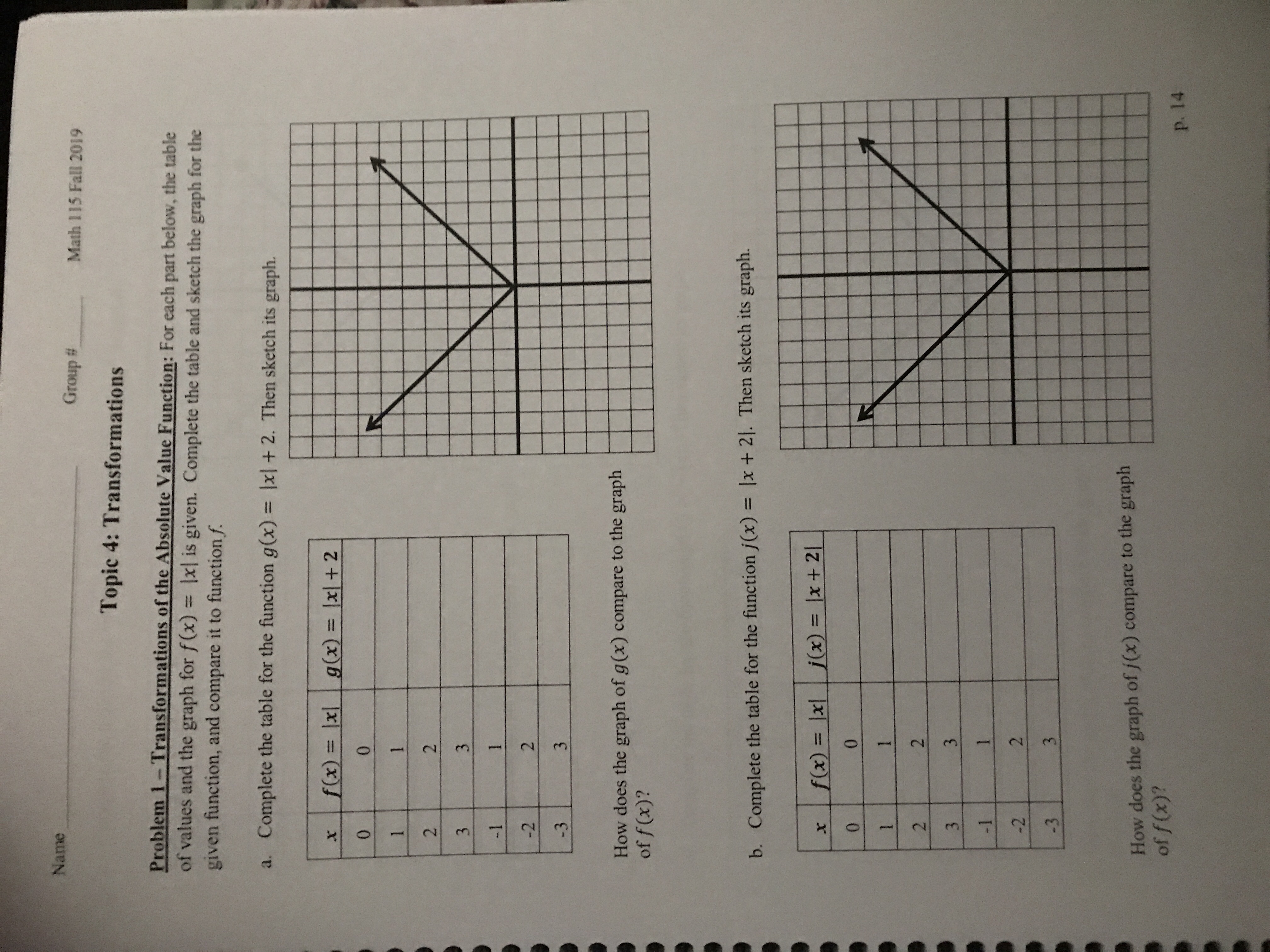
Answered Name Group Math 115 Fall 19 Topic Bartleby

L Hopital S Rule Wikipedia

L x L 3 L x 2 vBo= bxd bx bx(Lx) x, d d – 0 DT 0 3 DB 0 2 DB b 0 3 1 bL3 = ­ βBo, 6 D B bL bL2 4 vBoChelan by county tax code Clallam Clark by state tax code n Clark by county tax code "ً Columbia by state tax code # Columbia by county tax code !a Cowlitz by state tax code "U Cowlitz by county tax code Douglas R Ferry a Franklin } Garfield Grant by state tax code Grant by county taxThe Fourier transform we'll be int erested in signals defined for all t the Four ier transform of a signal f is the function F (ω)= ∞ −∞ f (t) e −

The Cbc Method

L 12 Start With The Formulas X Log E X And Chegg Com

Physics 505 Homework No 5 Solutions S51 1 Angular momentum uncertainty relations A system is in the lmeigenstate of L2, Lz (a) Show that the expectation values of L± = Lx ±iLy, Lx,10 Let f A!Rm be continuous and Asequentially compact Show f is uniformly continuous Solution Let fu kg, fv kgbe sequences in A such that fku k v kkg!0Suppose fkf(u k) f(v k)kg6!0Then along a subsequence, fkf(u n k) f(v n k)kg!c>0 (Why?) Since Ais sequentially compact, we can pick subsubsequences fuThe wave equation is Let y = X (x) T (t) be the solution of (1), where „X‟ is a function of „x‟ only and „T‟ is a function of „t‟ only Of these three solutions, we have to select that particular solution which suits the physical nature of the problem and the given boundary conditions Since we are dealing with problems on

Courses Maths Ox Ac Uk Node View Material 26

Deb Gpf3leuro Solopol Gfx Gritty Power Foam Refill Cartridge Carton Of 4 X 3 25l From Lawson His

Orthogonal collections • The norm of a vector kuk = p u2 1 ···u2 n = (u,u)1/2 • Orthogonality of two vectors u⊥ v iff (u,v) = 0 • Orthogonality of a collection of vectors {u 1,,um} is an orthogonal collection of vectors iff (ui,uj) = 0 if i 6= j • Orthogonal basis If m = n, the dimension of the space, then an orthogonal collection {u 1,,un} where ui 6= 0 for all iWORD Find and circle the words in the puzzle below R z x G B K J L U K e LOYALTY ewARR10R ewlNGMAN w00KlEE E H K B L z L M S F c W K E W c OUsing the wellknown Euler's formulas we can write the Fourier series of the function in complex form f (x) = a0 2 ∞ ∑ n=1(ancosnxbnsinnx) = a0 2 ∞ ∑ n=1(an einx e−inx 2 bn einx −e−inx 2i) = a0 2 ∞ ∑ n=1 an −ibn 2 einx ∞ ∑ n=1 an ibn 2 e−inx = ∞ ∑ n=−∞cneinx Here we have used the following

Chapter 7 Problems

G Shock X In4mation Glx 5600xa 4cr G Lide Surf Salmon Pink Buy Online At Consortium

Therefore, we have shown that (fg)(x h) (fg)(x) = (f(x)g0(x) g(x)f0(x))h r fg(h) (19) where jr fg(h)j jhj!0 as h!0Therefore, by the Landau de nition of di erentiability, we have shown that fgis di erentiable at every point x2Uand that its derivative is equal to f(x)g0(x)g(x)f0(x) = fDg gDfChristian Parkinson UCLA Basic Exam Solutions Linear Algebra 2 Hence T(y j) 2ker(S) for each jFurther if a 1;;a k2C are such that a 1T(y 1) a kT(y k) = 0;Then T(a 1y 1 a ky k) = 0 so a 1y 1 a ky k2ker(T) so there are b 1;;b '2C such that a 1y 1 a ky k= b 1v 1 b 'v ' =) a 1y 1 a ky k b 1v 1 b 'v '= 0 But these vectors form a basis for ker(S T) so in

Calculus Proofs Of Some Basic Limit Rules Wikibooks Open Books For An Open World

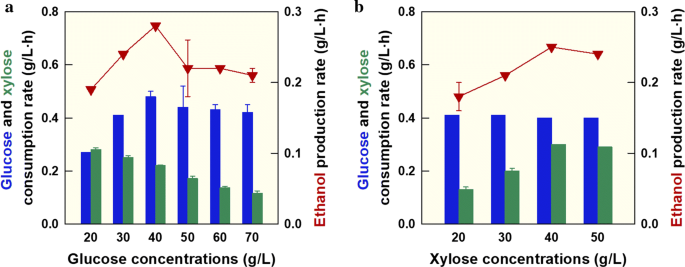
Alleviation Of Catabolite Repression In Kluyveromyces Marxianus The Thermotolerant Sbk1 Mutant Simultaneously Coferments Glucose And Xylose Biotechnology For Biofuels Full Text

 To find L (x) for a function g(x) at a point a you use this equation L(x) = g(a) g'(a)(x − a) The point we want is a = 2 so we need to find g(2) and g'(2) g(2) = 2 ⋅ f (22) About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators2) = L(x) L(y) Thus, condition 1 holds Moreover L(cxx) = L(cx 1,cx 2) = (cx 1,cx 2 −cx 1,cx 2) = c(x 1,x 2 −x 1,x 2) = cL(x) Since 1 and 2 hold, Lis a linear transformation from R2 to R3 The reader should now check that the function in Example 1 does not satisfy either of these two conditions Example 3 Define L R3 → R2 by L(x 1

Bayes Theorem With Change Of Measure Quantitative Finance Stack Exchange

Http Www Columbia Edu Ww40 Appendixno Pdf

37 Observação Para a definição do limite, quando x tende a a, não é necessário que a função esteja definida em a e pode ocorrer que a função esteja definida em a e lim f (x) f (a) x a z o O que interessa é o comportamento de f(x) quando x se aproxima de a e não o que ocorre com f quando x = a 33 Exemplos 1 Considere a função Taking the equation for the tangent line and solving for y, we observe that the tangent line is given by y = f′(a)(x − a) f(a) and moreover that this line is itself a function of x Replacing the variable y with the expression L(x), we call L(x) = f′(a)(x − a) f(a) the local linearization of f at the point (a, f(a))That is, prove that if l(x) l'(x) g(x)f'(x)f(x)g'(x) (g(x))?

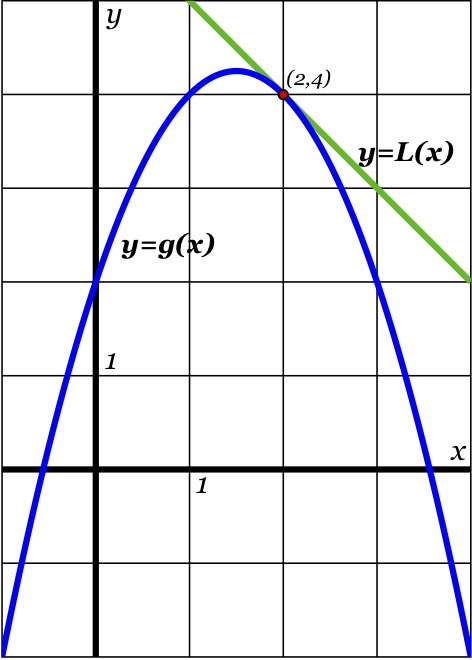
Cc The Tangent Line Approximation

Http Silverstripe Fkit Hr Cabeq Assets Uploads Cabeq 16 01 2269 Pdf

1Find the mass of a rod of length 10 cm, with lineal density (x) = e x g/cm, where xis the distance in cm from the left end of the rod Since the density is e xg/cm, the mass of each thin slices of the rod will be e x x Units (g/cm) cm = g Total mass = Z 10 0 e xdx= e x 10 0 = 1 e 10 ˇ g 2A rod is 2 meters long

Production Of Added Value Metabolites By Yarrowia Lipolytica Growing In Olive Mill Wastewater Based Media Under Aseptic And Non Aseptic Conditions Sarris 17 Engineering In Life Sciences Wiley Online Library

Lesson 4 Calculating Limits

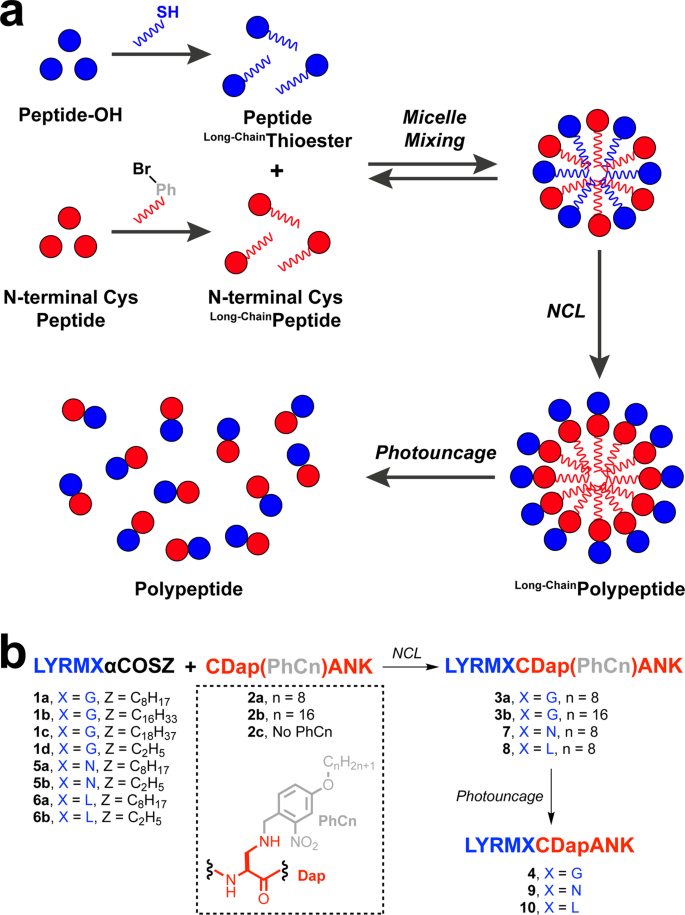
Traceless Native Chemical Ligation Of Lipid Modified Peptide Surfactants By Mixed Micelle Formation Nature Communications

Kinetic Analysis And Mathematical Modeling Of Growth And Lactic Acid Production Of Lactobacillus Casei Var Rhamnosus In Milk Whey Sciencedirect

Stacking Benches Furniture Products Ypo

Neil Strickland Staff Shef Ac Uk Courses Mas243 Lectures Handout04 Pdf

Men S Black Cp Company X G Foot Arm Lens Tour Jacket Size L Illustrated Lining 169 00 Picclick Uk

Aviation Photographs Of Registration Vh Xgl Abpic

Thetford Campa Potti Qube Xgl Organic Toilet Portable Camping 21l Amazon Co Uk Sports Outdoors

Linear Approximation And Differentials In Calculus Owlcation

Mettler Pl2 L 00 Balance 210g X 0 01g Lab Unlimited Uk

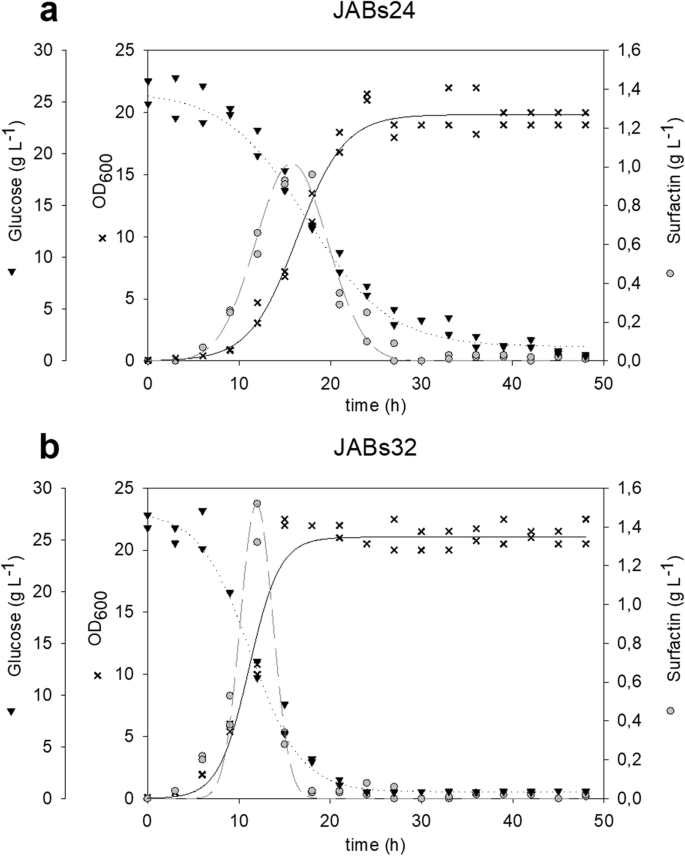
Bacillus Subtilis High Cell Density Fermentation Using A Sporulation Deficient Strain For The Production Of Surfactin Springerlink

Help Understanding Proof Of L Hospital S Rule From Rudin Mathematics Stack Exchange

4 X Mannol Hypoid 4l Gear Oil Sae 80w 90 Api Gl 4 Gl 5 Ls Mil L 2105 D 16 Litres For Sale Online Ebay

Lancome L Absolu Rouge Lipstick Set 3 X 3 4g Hogies

L Carnitine X 100g Nutri Link

Quick Select Clarification Stack Overflow

Cc The Tangent Line Approximation

Growth Overview Microbial Growth Overview Of Terms Exponential

Shelf And Shelving Accessories For Box15 Shelving System Kit

Exhibition Stands Corner Stands Pop Up Displays

Http Maths Dur Ac Uk Dma0wjz B1 Anlec1 Pdf

Preventa 85ppm Deuterium Depleted Water

Simple Harmonic Motion Ppt Video Online Download

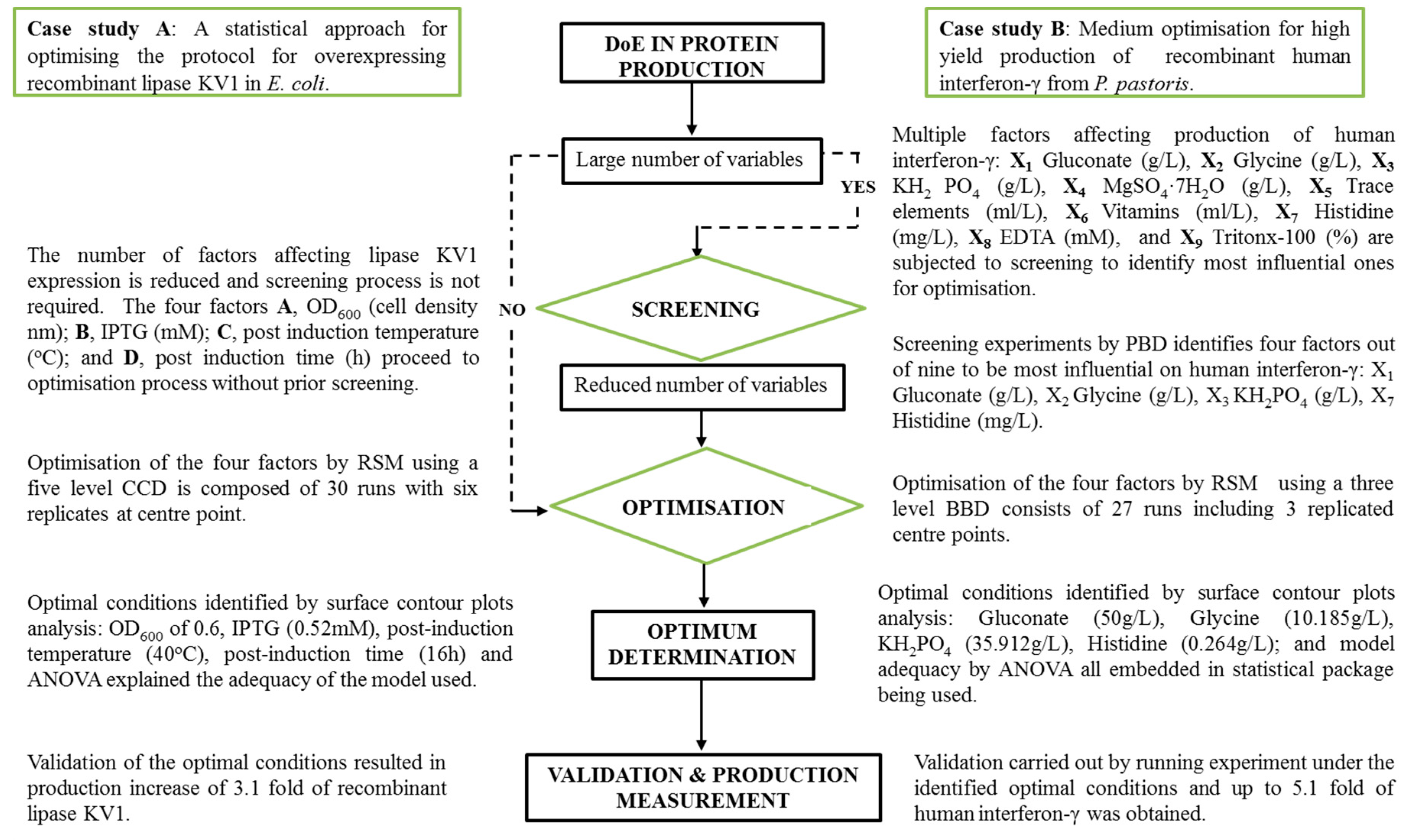
Bioengineering Free Full Text The Goldilocks Approach A Review Of Employing Design Of Experiments In Prokaryotic Recombinant Protein Production Html

Lancome L Absolu Rouge Lipstick Set 3 X 3 4g Hogies

1 How Many Moles Of Ozone Occupy A Volume Of

Answered If Lim F X L And Lim G X L Bartleby

L Hopital S Rule Introduction Video Khan Academy

Hfy G Warm Coat For Dogs Autumn And Winter Plus Velvet With Ball Cap For Hair Two Legs Sweater S M L Xl Yellow X Large Yellow Amazon Co Uk Kitchen Home

G L L 00 E Bass Guitar Original 19 Advertisement 8 X 11 Ad With Specs Gl Bass Guitar Guitar Fender Bass Guitar

G Sr Large Gaming Mouse Pad For Esports Zowie Uk

2

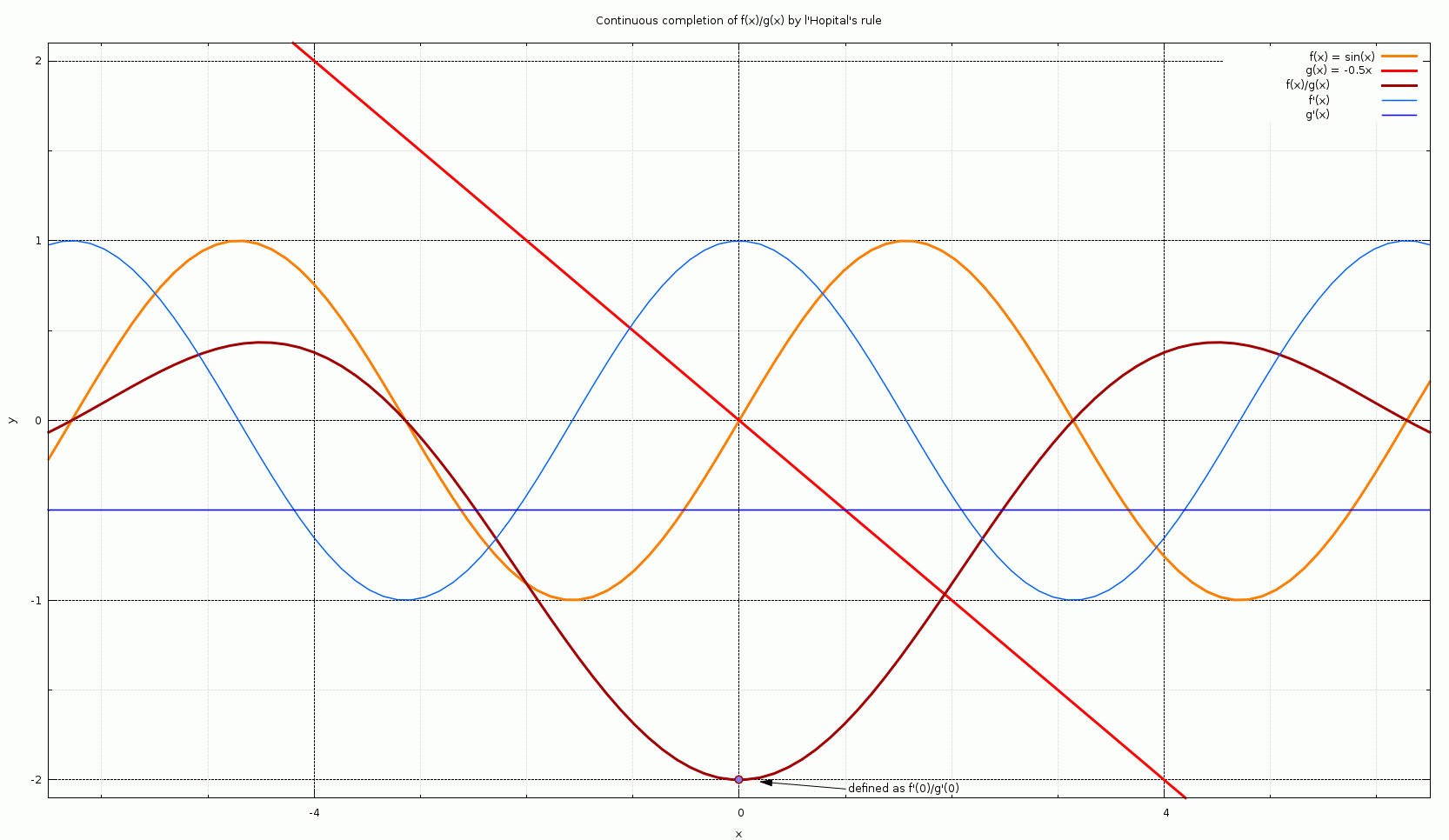
L Hopital S Rule Wikipedia

Scopri La Nostra Collezione Di Selle Selle Italia

Growth Overview Microbial Growth Overview Of Terms Exponential

Xgl Wikipedia

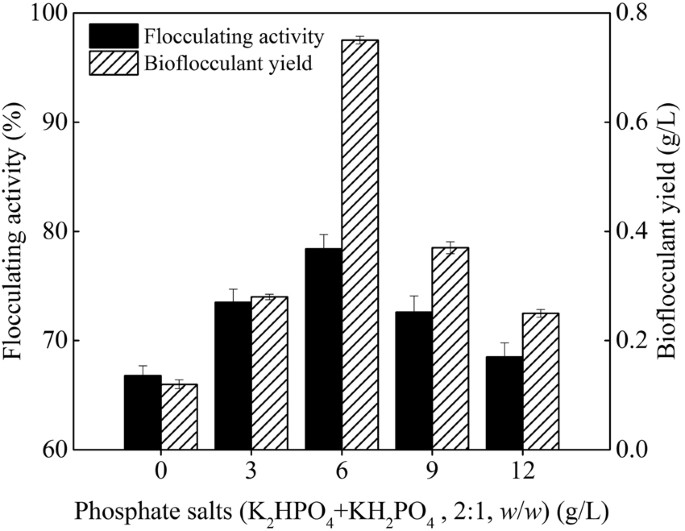
Fermentation And Kinetics Characteristics Of A Bioflocculant From Potato Starch Wastewater And Its Application Scientific Reports

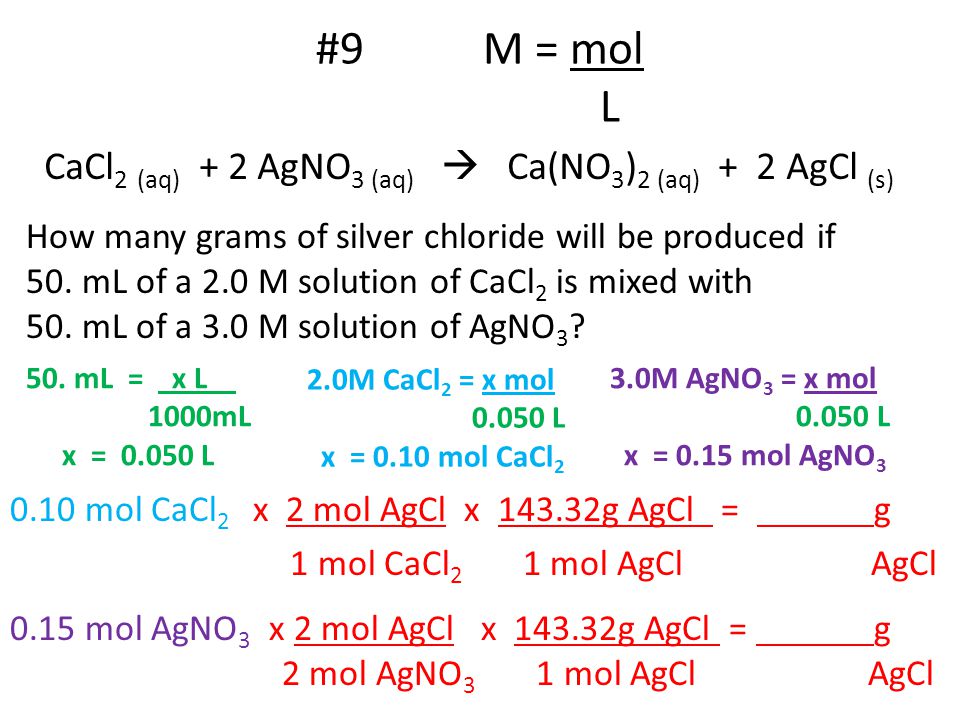
Molarity Calculation Practice 1 M Mol L What Is The Concentration Of A Solution With 0 25 Mol Of Solute In 0 75 L Of Solution M 0 25 Mol Ppt Download

Bayes Theorem With Change Of Measure Quantitative Finance Stack Exchange

I Have H2o2 Of Molecular Wt 34 01gm And 30 W V What Does It Mean That I Am Not Getting It And I Want To Prepare 0 1m Solution How Can I

Ocw Mit Edu Resources Res 18 007 Calculus Revisited Multivariable Calculus Fall 11 Study Materials Mitres 18 007 Supp Notes03 Pdf

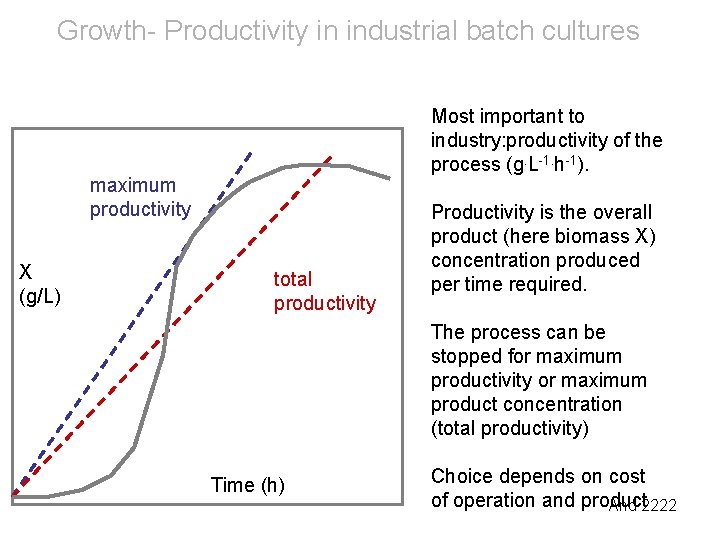
Growth Overview Microbial Growth Overview Of Terms Exponential

Diamond Paste Set 3 Syringes 000 Grit X 5 G L 10 Concentration Ebay

Limite Functions Sect22 24

Chemical Equilibrium What Is Equilibrium Expressions For Equilibrium

Www cb Asn Au Documents Item 4621

Growth Overview Microbial Growth Overview Of Terms Exponential

Pdf A Cultivation Technique For E Coli Fed Batch Cultivations Operating Close To The Maximum Oxygen Transfer Capacity Of The Reactor

Bank Reconciliation Accounts In S 4hana Sap Blogs

Wholesale Cosmetics 6 X L Oreal Double Extention Waterproof Black Mascara

1 1 2 Properties Of Limits

X Keys L Trac Blue Trackball Keyboard Specialists Ltd

Engineering Mathematics Ii Ma Ppt Download

Http Publications Ut Capitole Fr 1 Laffont Pdf

Http Publications Ut Capitole Fr 1 Laffont Pdf

X Keys L Trac Blue Trackball Keyboard Specialists Ltd

Cobra Men S Microgrip Flex Golf Gloves S M Ml L Xl X 3 Bulk Mens Ebay

Rhodosporidium Toruloides Cultivated In Nacl Enriched Glucose Based Media Adaptation Dynamics And Lipid Production Tchakouteu 17 Engineering In Life Sciences Wiley Online Library

Kinetic Analysis And Mathematical Modeling Of Growth And Lactic Acid Production Of Lactobacillus Casei Var Rhamnosus In Milk Whey Sciencedirect

Kerastase Cure Intensive Anti Chute A L Aminexil Gl Treatment 0 2 X 10 Amazon Co Uk Beauty

Can Ppm Be Converted To Mg L

Mazda 3 Hatchback 2 0 Skyactiv X Mhev 186 Se L Lux 5dr Lease Select Car Leasing

Physics 101 Lecture Elasticity And Oscillations Ppt Download

Polyform G2 Fender 407mm L X 117mm D Boat Fenders Direct Limited

Www Jstor Org Stable

96 X 100g Pedigree Mixed Pack 28x Dentastix L Special Bundle Price Zooplus Co Uk

Theorem For Limits Of Composite Functions Video Khan Academy

Incoming Term: lim f(x).g(x) = l.m,